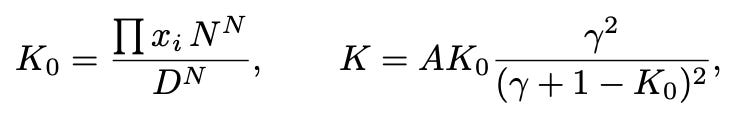Two Types Of Concentrated Liquidity.
Concentrated Liquidity.
Welcome, premium subscribers! Thank you for subscribing. What will be shared today and the days ahead are alpha from our Economics Design's researchers.
Please keep these mails secret and do not share them with any one because these alphas are confidential. Enjoy your reading.
TLDR below. This is not financial advice.
General Conclusion
Both Curve V2 and Uniswap V3 have many outstanding improvements in the recent update. Both focus on how to improve capital and capital efficiency. They have done so by refining the AMM model and concentrated liquidity mechanism.
Changing the AMM model also helps protocols create new "games" in capital management. We will discuss this and how the build protocols on Uniswap and Curve evolved. Meanwhile, concentrated liquidity helps to increase liquidity and reduce slippage.
Uniswap V3
Concentrated Liquidity
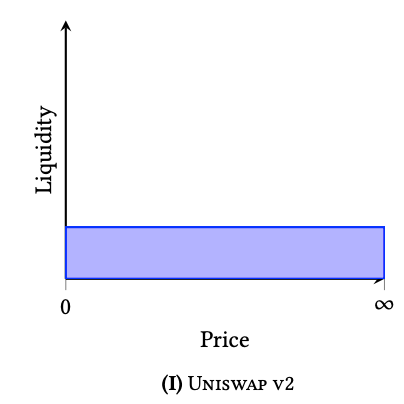
Concentrated liquidity is one of the most prominent innovations in Uniswap V3, an improvement on the lack of efficiency in the x*y = k model.S
In the xy=k model, you can swap one token and get the other at any price point, that is, the liquidity on the xy*=k* model will spread for any price from 0 to infinity, because at any price we can exchange 1 token for another token with the amount corresponding to the price there.
But on closer inspection, this model creates a waste of liquidity.
For example: In Uniswap V2, if we spend $1000 to provide liquidity for a stablecoin pair like DAI/USDT, pairs like this usually only fluctuate in the range of [0.99;1.01]. The liquidity reserve in this price range is about 0.5%, or $5 ($1k capital), which is the amount that is operated for which fees can be collected. The remaining $995 will be inactive and will not collect transaction fees because the price cannot be traded outside of the upper range [0.99; 1.01].
We can see that the sources outside this price range (P < 0.99 or 1.01 < P) will not be used. This leads to a waste of liquidity.
Uniswap V3 was created with a concentrated liquidity feature to solve this problem.
Thanks to the concentrated liquidity feature, liquidity providers can focus on providing liquidity within the desired price range or the price range they think will earn the most fees. For example, the DAI/USDT pair trades only in the range of 0.99 – 1.01. Liquidity providers can choose to provide liquidity for this pair in the price range of only 0.99-1.01.
Uniswap V3 AMM Model
When we consider providing liquidity for a pair of tokens X and Y, we can select the price range [Pa; Pb] we want to provide liquidity. With the current price of P, Uniswap V3 will determine the exact number of X and Y tokens respectively required to add to the pool, according to this formula:
Where:
X is the number of tokens X Y is the number of tokens Y Pa is the lowest price of the price range Pb is the highest price of the price range L is the liquidity constant.
When a trade occurs, the current price moves. All liquidity providers collect a portion of trading fees based on the liquidity rate they provide at the moving price range. The smaller the price range (if the market price is in range), the higher the percentage of fees that can be earned by liquidity. However, the smaller the price, the easier it is for the price to break out of the range, the liquidity position to close, and for thereto be no collection of fees. Until the price returns to the price range, their position will continue to work and collect fees.
Assumption 1: There are two liquidity providers A and B, providing liquidity for ETH-USDC pair (X is $ETH and Y is $USDC). The current price of $ETH is $4000. Both provide a source of liquidity with a value of $100,000.
A chooses to provide liquidity on V3, with the price A wants to offer being [3,600; 4,200]. Based on the above formula, we can calculate the amount of liquidity (L) provided by A to be 2,096.
B chooses to provide liquidity on V2, So the price B offers will be [0; ∞]. We can calculate that the L provided by B is 79.
From here we can conclude, with the same amount of liquidity spent, that the amount of liquidity that A can collect in transaction fees is 2,096/79 = 26.5 times higher than that of B when the price moves between [3,600; 4,000].
Assumption 2: There is a liquidity provider C, with a liquidity value of $1000, choosing to provide liquidity in the range [3,800; 4,100]. And the current price is also $4,000. We can calculate that the amount of liquidity that C provides is 4,206.
We see that with the same liquidity, the amount of liquidity that C can collect is 4,206/2,096 = 2 times higher than A when the price moves in the range [3,800; 4,100]
From the above two examples, we can conclude that V3 helps to increase the efficiency of using the capital of liquidity providers. With the same amount of liquidity, the smaller the price, the greater the percentage of fees that the LP can collect. In addition, this mechanism helps create liquidity management projects directly on Uniswap V3 such as Visor Finance, a protocol that helps the LPer manage liquidity easily, and optimise fees received.
Benefits
For the user: Liquidity will be more abundant in the converging price area, thus reducing slippage.
For teh liquidity provider: You can freely choose the liquidity area you want and focus on providing the liquidity where the price zone is moving so that you can collect the best fee rate. This minimises risk when providing liquidity.
For example, when the price of one of the two tokens goes to $0, liquidity provider V3 will lose less capital than V2 because, for the same liquidity depth at a price zone, V2 must provide larger liquidity to achieve the same liquidity depth as V3 at a certain price range. That leads to a higher risk of capital loss that V2 bears compared to V3.
Curve V2
Concentrated Liquidity
On Curve V2, concentrated liquidity doesn’t require manual repegging. LPers concentrate liquidity given by the current ‘internal oracle’ price, but only move that price when the loss is smaller than part of the profit which the system makes.
This creates 5-10 times higher liquidity than the Uniswap invariant, as well as higher profits for liquidity providers
Curve has a price oracle given by an EMA applied in N-dimensional price space. The formula is:
Where the last reported price is Plast, and the update happened t seconds ago while the half-time of the EMA is T1/2.
Curve V2 AMM Model
Along with the same idea, Curve V2 also developed a new AMM model that helps to reduce slippage, while creating a liquidity depth of 5-10 times compared to Uniswap V3, as well as higher nightly income for LPers.
Curve AMM is called AMM with dynamic peg, which has the formula:
Curve define K slightly differently with AMM V1:
Where A is the amplification coefficient, and γ > 0 (but usually a small number) has a meaning of the distance between the two dashed curves below. The invariant works approximately as a superposition of constant-product and stableswap invariants.
constant-product (dashed line), stableswap (blue) and from this work (orange)
The upgrade essentially allows low-slippage swaps between volatile pairs of assets or between assets that have constantly fluctuating prices.
Dynamic Fee
All the vaults in Curve share the same dynamic fees program. The program determines a fee (f) ranging from f_mid to f_out:
The core algo of the fee program runs with these goals:
High market volatility: Higher LP fees, reducing IL and capturing higher profits
Low market volatility: Lower LP fees to encourage trading
Benefits
For the user: Liquidity will be more abundant in the converging price area, thus reducing slippage.
For the liquidity provider: You can freely choose the range price, by means of the repegging mechanism. This is really convenient for 'lazy' LPers while still ensuring you can collect the best fee.
TLDR:
Obviously both Curve V2 and Uniswap V3 focus on better capital use issues. However, they have different effects because the goals of each protocol are different: Uniswap's AMM is used for any transaction, and Curve's AMM is used for assets of the same anchor price. This gradually leads to different ways of allocating funds.